2019. 4. 22. 22:11ㆍAlgorithm/이론
특징
1. 트리는 하나의 루트 노드를 갖고있다.
2. 루트 노드는 2개 이하의 자식노드를 갖고 있다.
3. 그자식 또한 2개 이하의 자식노드를 갖고있고 이는 반복적으로 정의 된다.
노드들과 다른 노드들을 연결하는 간선으로 구성되어있다.
일반적으로 아래와 같은 모습으로 이루어져있다.
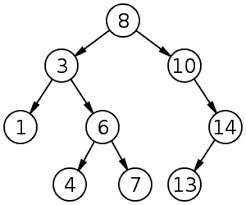
자식은 2개가 있어도 되고 없어도 되고 한개만 있어도 된다. 모든 노드들에 상응한다.
방법은 일반적으로 배열과 연결리스트 와 같은 방식으로 구성된다.
배열은 크기가 제한적이고 빈칸이 생길 수 있다. 그렇지만 쉽고 간단하게 표현할 수 있다.
용어 정리
Root: 제일 상위 노드
부모-자식 관계: 노드의 상위 노드가 부모이고 그 밑의 노드를 자식이라고 한다.
형제: 부모가 동일한 노드들을 형제라고 부른다.
leaf: 자식이 없는 노드들을 leaf라고 부른다.
조상-자손 관계: 1세대를 뛰어 넘어 상위 노드와 하위노드를 뜻한다.
서브트리 : 하나의 노드와 자손의 노드들로 이루어진 트리를 부트리라고 한다.
완전 이진 트리: 차례대로 채워나가는 방식이다.
높이는 log(n)
풀 이진 트리: 꽉꽉 채워져있는 트리이다.
노드의 수는 2^h -1이다. 완전 이진트리는 차례대로 차곡차곡 쌓이게핸다.

다른 이진 트리: 데이터가 같다고 만해서 같은 이진 트리가 아니라 서로 다른 이진트리이다.

순회 방법은 4가지가 있다.
Inorder, PostOrder, PreOrder, levelOrder

1. Inorder
Left Root Right
제일 왼쪽의 노드 부터 출력 후 자기자신 오른쪽을 출력해주면 된다.
1 3 4 6 7 8 10 13 14
void inOrder(Node* node){
if(node != NULL){
inorder(node->left);
printf("%d", node->value);
inorder(node->right);
}
}
2. preOrder
Root Left Right
가운데 값부터 출력후 왼쪽 출력하고 오른쪽 순으로 출력된다.
8 3 1 6 4 7 10 14 13
void preorder(Node* node){
if(node != NULL){
printf("%d", node->value);
preorder(node->left);
preorder(node->right);
}
}
3. PostOrder
Left Right Root
왼쪽 부터 출력 후 오른쪽 출력 후 가운데 출력해주면 된다.
1 4 7 6 3 13 14 10 8
void postOrder(Node* node){
if(node != NULL){
postOrder(node->left);
postOrder(node->right);
printf("%d", node->value);
}
}4. levelOrder
1level 2level 3level 순으로 된다.
8 3 10 1 6 14 4 7 13
사용해주기 위해서는 queue를 사용해주어야한다.
qu가 빌때까지 하나의 노드의 방문시 left, right를 넣어주고 pop()해주고를 반복해준다.
void levelOrder(Node *root)
{
qu.push(root);
while (!qu.empty())
{
Node *node = qu.front();
printf("%d", node->value);
qu.pop();
if (node->left != NULL)
qu.push(node->left);
if (node->right != NULL)
qu.push(node->right);
}
}'Algorithm > 이론' 카테고리의 다른 글
| (3)최소 비용 신장 트리(MST) Kruskal 알고리즘 (0) | 2019.05.20 |
|---|---|
| (2)최소 비용 신장 트리(MST) Generic MST (0) | 2019.05.20 |
| (1)최소 비용 신장 트리(MST) 기본이론 (0) | 2019.05.20 |
| Hashing (0) | 2019.04.29 |
| 이진 탐색트리 (0) | 2019.04.24 |