2020. 2. 1. 18:09ㆍAlgorithm/문제풀이
LIS 알고리즘
https://www.acmicpc.net/problem/11053
11053번: 가장 긴 증가하는 부분 수열
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.
www.acmicpc.net
문제는 간단하다. 아래와 같은 수열 중 부분수열 중 길이가 증가하면서 가장 긴 부분수열을 구하는 문제이다.
{10, 20, 10, 30, 20, 50} => {10, 20, 30, 50}
푸는 방법이 이진 탐색을 사용하여 O(nlogn)이 걸리는 방법 dp를 사용하는 방법O(n^2) 두가지가 있다. 이 글은 dp로 문제를 해결해보겠다.
{10, 20, 10, 30, 20, 50}
index 0 1 2 3 4 5
i, j로 index를 잡아 i 밑의 값의 index인 j와 비교하여 i보다 크다면 +1 작다면 넘어가며 새롭게 +1되는 값이 기존과 다른 최고의 값인지 확인해야한다. 그래서 점화식은
if(arr[i] > arr[j] && dp[i] < dp[j]+1) // j까지의 방법보다 더 큰 방법이 있다면 +1
dp[i] = dp[j] + 1;
#include <cstdio>
#include <algorithm>
using namespace std;
int N;
int arr[1002];
int dp[1002];
int main(){
scanf("%d", &N);
for(int i = 0; i < N; i++)
scanf("%d", &arr[i]);
for(int i = 0; i < N; i++){
dp[i] = 1;
for(int j = 0; j < i; j++){
if(arr[i] > arr[j] && dp[i] < dp[j] + 1)
dp[i] = dp[j] + 1;
}
}
printf("%d", *max_element(dp, dp+N));
}
LIS를 활용한 문제 가장 긴 바이토닉 부분 수열
https://www.acmicpc.net/problem/11054
11054번: 가장 긴 바이토닉 부분 수열
첫째 줄에 수열 A의 크기 N이 주어지고, 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ N ≤ 1,000, 1 ≤ Ai ≤ 1,000)
www.acmicpc.net
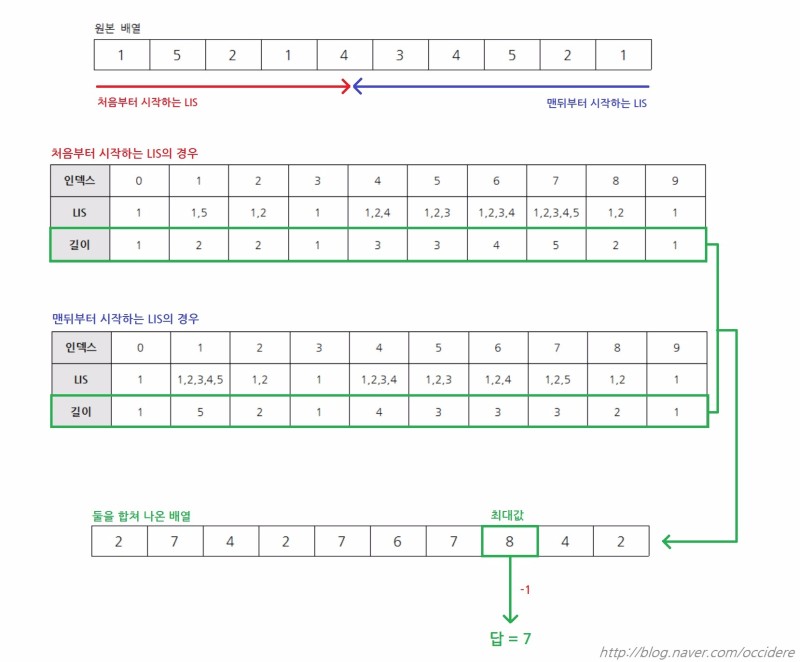
이문제는 요소의 값이 증가하다가 다시 감소하는 최장의 수열을 구하는 문제이다. 위의 문제를 잘 활용하여 쉽게 풀수있다.
기존과 같이 처음부터 증가하는 수열하나 뒤부터 증가하는 최장 수열을 구해 서로 공통되는 index의 값을 더한 후 -1을 해준 것의 최대값이 문제의 답이된다.
#include <cstdio>
#include <algorithm>
using namespace std;
int arr[1002];
int dp[3][1002];
int maxArray = 0;
int main(){
int N;
scanf("%d", &N);
for(int i = 0; i < N; i++)
scanf("%d", &arr[i]);
for(int i = 0; i < N; i++){
dp[0][i] = 1;
for(int j = 0; j < i; j++){
if(arr[i] > arr[j] && dp[0][i] < dp[0][j] + 1)
dp[0][i] = dp[0][j] + 1;
}
}
for(int i = N-1; i >= 0; i--){
dp[1][i] = 1;
for(int j = N-1; j > i; j--){
if(arr[i] > arr[j] && dp[1][i] < dp[1][j] + 1)
dp[1][i] = dp[1][j] + 1;
}
}
for(int i = 0; i < N; i++)
if( maxArray < dp[0][i] + dp[1][i] - 1)
maxArray = dp[0][i] + dp[1][i] - 1;
printf("%d", maxArray);
}
'Algorithm > 문제풀이' 카테고리의 다른 글
| 백준 2004 조합 0의 개수 (0) | 2020.02.20 |
|---|---|
| dp 백준 9251 LCS (0) | 2020.02.02 |
| dp 백준 2156 포도주 시식 (0) | 2020.02.01 |
| dp 백준 쉬운 계단 수 10844 (0) | 2020.02.01 |
| dp 백준 1463 1로 만들기 (0) | 2020.01.31 |