2020. 4. 11. 21:41ㆍAlgorithm/이론
최단 경로(3) 벨만 포드
벨만포드는 다익스트라와 다르게 각 정점을 하나씩 제외하면서 우선순위 큐에 넣는 것이아닌 입력된 모든 path를 반복문 돌려서 최단 경로를 구할 수 있다.
또한 다른 알고리즘과 다르게 -가중치의 값또한 해결할 수 있다. 하지만 -가중치로 인한 계속 -가되는 -cycle이 생성될 수 있다. 그러므로 알고리즘을 작성한 후 -cycle이 존재하는지 체크해야할 필요가 있다.
그리고 다른 최단거리 알고리즘과 Relax 함수는 비슷하다.
if(vertex[end] > vertex[start] + map[start][end])
vertex[end] = vertex[start] + map[start][end];초기 정점의 설정 값은 INF로 설정해준다. 만약 알고리즘을 돌다가 시작점이 INF라면 무시해주어도 된다. 시작점이 INF로 다른 도착점에 도착할 수 없기 때문입니다.
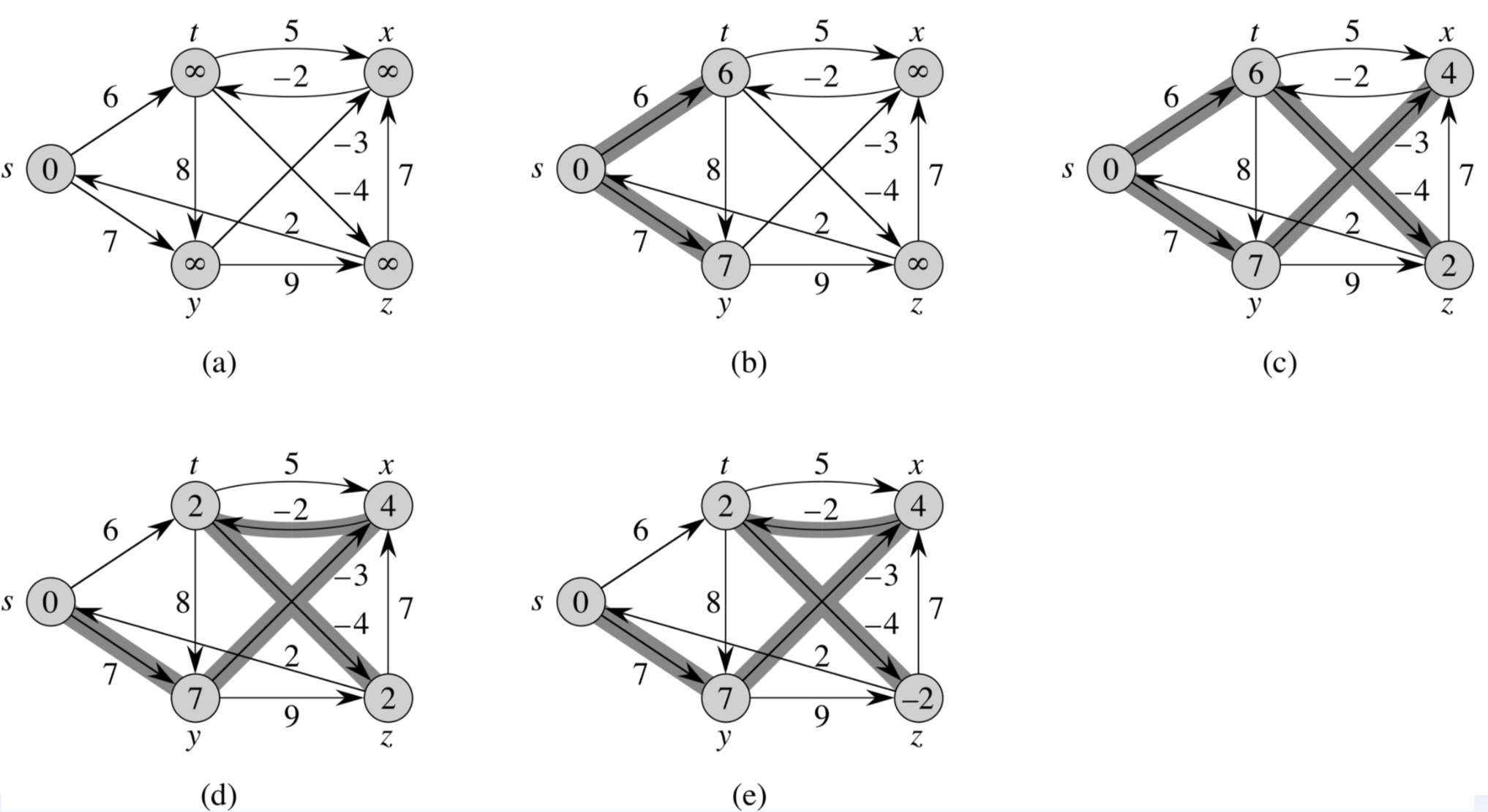
위 사진을 보면 초기 s에서 시작하여 s와 연결된 다른 정점들의 값을 바꾸어 나갑니다. 이와 같은 반복을 정점의 개수만큼 실행해주면 됩니다.
sudo 코드

첫 반복문은 각 정점의 수만큼 진행해주고 두번째 반복문은 존재하는 간선의 개수 만큼 실행해줍니다. Relax함수는 출발점에서 종료점까지의 비교를 하며 교체해 나갑니다.
마지막 반복문은 -cycle을 구하는 방법입니다. -cycle이 존재한다는 의미는 이미 구해진 최단 경로에서 한번이라도 Relax 연산이 이루어질 수 있다면 이는 -cycle이 존재한 다는 뜻이니 최단 경로를 구할 수 없다고 결과를 내립니다.
벨만포드를 응용한 문제 타임머신
https://www.acmicpc.net/problem/11657
11657번: 타임머신
첫째 줄에 도시의 개수 N (1 ≤ N ≤ 500), 버스 노선의 개수 M (1 ≤ M ≤ 6,000)이 주어진다. 둘째 줄부터 M개의 줄에는 버스 노선의 정보 A, B, C (1 ≤ A, B ≤ N, -10,000 ≤ C ≤ 10,000)가 주어진다.
www.acmicpc.net
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
int INF = 987654321;
int N, M;
int map[502][502];
int vertex[502];
vector <pair<int, int> > vec;
void ford();
void input();
int main(){
input();
ford();
for(int line = 0; line < vec.size(); line++){
pair<int, int> info = vec[line];
int start = info.first;
int end = info.second;
if(vertex[start] == INF)
continue;
if(vertex[end] > map[start][end] + vertex[start]){
printf("-1");
return 0;
}
}
for(int i = 2; i <= N; i++){
if(vertex[i] == INF)
printf("-1\n");
else
printf("%d\n", vertex[i]);
}
}
void input(){
int a, b, c;
scanf("%d %d", &N, &M);
for(int i = 0; i < M; i++){
scanf("%d %d %d", &a, &b, &c);
if(map[a][b] == 0){
map[a][b] = c;
vec.push_back(make_pair(a, b));
}
else
map[a][b] = min(map[a][b], c);
}
for(int i = 1; i <= N; i++)
vertex[i] = INF;
vertex[1] = 0;
}
void ford(){
for(int ver = 1; ver <= N; ver++){
for(int line = 0; line < vec.size(); line++){
pair<int, int> info = vec[line];
int start = info.first;
int end = info.second;
if(vertex[start] == INF)
continue;
if(vertex[end] > map[start][end] + vertex[start]){
vertex[end] = map[start][end] + vertex[start];
}
}
}
}
'Algorithm > 이론' 카테고리의 다른 글
| union-find(Disjoint-set) (0) | 2020.06.25 |
|---|---|
| 투포인터(two pointer) (4) | 2020.05.10 |
| 최단거리(2) 플로이드 (0) | 2020.04.11 |
| 최단 거리(1) 다익스트라 알고리즈 (0) | 2020.04.11 |
| DP(2) (0) | 2019.06.03 |