2020. 6. 25. 09:07ㆍAlgorithm/이론
union-find(Disjoint-set)
union-find(Disjoint-set)은 데이터들을 하나의 집합으로 묶어 표현할 필요가 있을 때 사용된다. 예를 들어 게임에서 하나의 파티를 표현하고 싶을 때 같은 1번 파티라는 것을 표현하기 위해 사용된다.
이와 같은 연산을 하기 위해서 필요한 3가지 연산이 있습니다.
1. 초기화(init): 초기에는 특별한 집합이 없는 자기 자신을 가리키는 초기화를 만듭니다.
2. 합치기(union): 두 원소 a와 b가 주어졌을 때 이 둘을 하나의 집합으로 만듭니다.
3. 찾기(find): 해당 원소가 어떤 집합에 속해있는지 찾습니다.
이러한 집합을 표현하는데 있어서 가장 쉬운 방법은 트리를 이용한 것입니다. 트리에서 한 집합에 속하는 원소들을 하나의 트리로 묶어줍니다. 따라서 union find는 tree를 통해 하나의 집합에 속해있다 판단할 수 있습니다.

위 사진과 같이 존재할 때 어떤 집합에 속해있는지 알기 위해서는 root를 확인하면 됩니다.
- 만약 0, 1이 같은 집합에 속해있는지 확인합니다. 위 사진에서는 0, 1의 root가 동일한 2임으로 결론적으로 같은 집합에 속하게 되는 것입니다.
- 또한 union 연산을 진행하는 것 또한 간단합니다. 특정 원소 둘의 루트를 찾은 다음 하나를 다른 한쪽의 자손으로 넣어 주면 됩니다.
(넣기 전에 find 연산을 통해 root를 찾아주어야합니다.)
구현 코드
int parent[100000];
void init(){ // 초기에는 자기 자신을 root로 초기화 시켜준다.
for (int i = 1; i<= 100000; i++)
parent[i] = i;
}
int find(int a){
if(a == parent[a])
return a;
return find(parent[a]);
}
void merge(int a, int b){
a = find(a), b = find(b);
if (a == b)
return;
parent[a] = b;
}
그런데 여기서 find 연산을 실행시키면 트리의 높이만큼 비례하여 연산이 진행됩니다.

위와 같이 그래프가 한쪽으로 귀울어 질 때 높이에 비례하여 연산이 진행됩니다. O(n) 탐색 시간이 걸립니다.
따라서 위와 같은 문제를 해결하기 위해 아래 방법을 이용합니다.
- 낮은 높이를 가진 트리를 높은 높이를 가진 트리에 집어 넣습니다.

이전 사진 2 - 0 - 1 트리가 옆 트리보다 작기 때문에 루트가 5인 트리에 넣어줬을 때 이전과 같이 높이는 3이 되었습니다. 반면 크기가 작은 2 - 0 - 1 트리에 루트가 5인 트리를 넣어줬을 때는 전체 길이가 4가 되어 왼쪽과 비교했을 때 연산 시간이 더 올래 걸릴 것 입니다.
- find 연산 중 root를 찾은 후 재귀 중 방문했던 노드들의 부모를 root로 바꿔 줍니다.
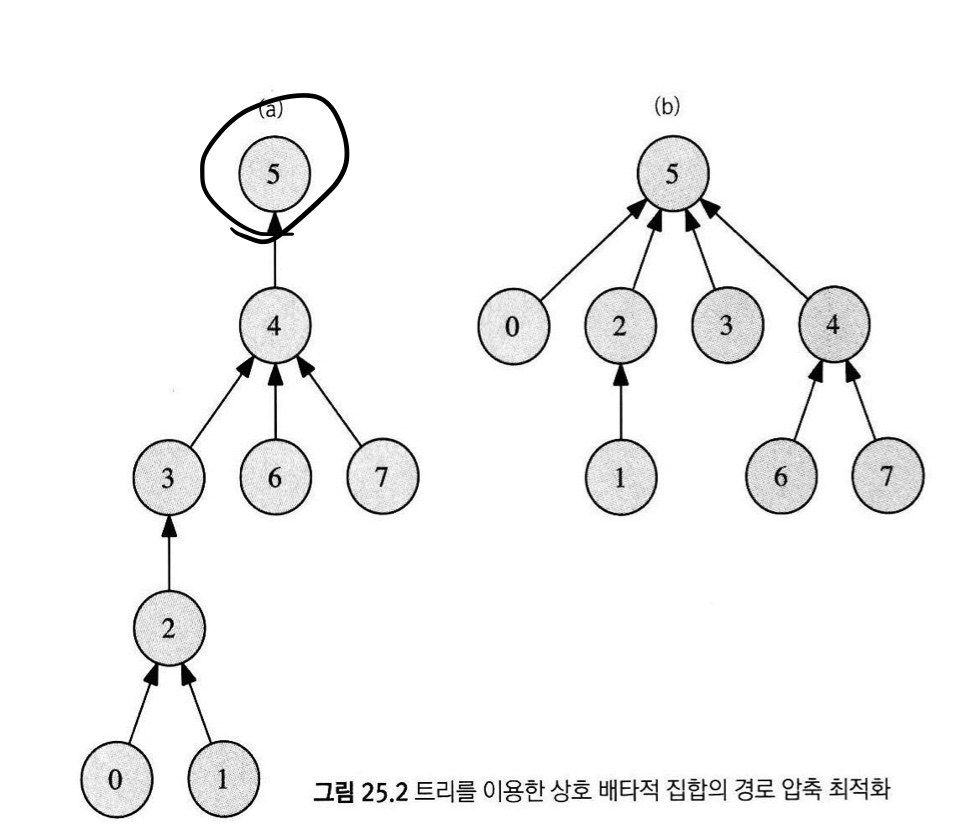
위 사진에서 find(0)을 진행해줄 때 5를 root로 찾은 다음
2의 부모를 3이 아닌 5로 바꾸고 3의 부모를 4가 아닌 5로 바꾸어서 전체적인 높이를 3으로 줄였습니다.
최적화 된 코드
int parent[10000], rank[10000];
void init(){
for(int i = 1; i <= 10000; i++)
parent[i] = i;
}
// root를 반환한다.
int find(int a){
if(a == parent[a])
return a;
return parent[a] = find(parent[a]);
}
void merge(int a, int b){
a = find(a), b = find(b);
// a, b가 같은 집합이면 함수 종료한다.
if (a == b)
return;
if (rank[a] > rank[b]){
int temp = a;
a = b;
b = temp;
}
// 항상 a의 높이가 더 낮기 때문에 a의 부모에 b를 넣는다.
parent[a] = b;
if (rank[a] == rank[b]) rank[b]++;
}'Algorithm > 이론' 카테고리의 다른 글
| 트라이 (0) | 2020.07.18 |
|---|---|
| KMP 알고리즘 (0) | 2020.07.17 |
| 투포인터(two pointer) (4) | 2020.05.10 |
| 최단 경로(3) 벨만 포드 (0) | 2020.04.11 |
| 최단거리(2) 플로이드 (0) | 2020.04.11 |