2020. 7. 18. 02:37ㆍAlgorithm/이론
트라이는 문자열의 집합을 표현하는 트리 자료 구조로, 집합 내에서 원하는 원소를 찾는 작업을 O(M) 시간만에 할 수 있습니다.
문자열 집합 S={"BE", "BET", "BUS", "TEA", "TEN" }를 저장하는 트리의 예는 아래와 같습니다.
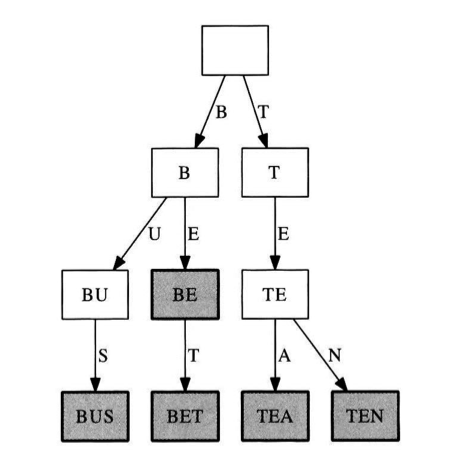
여기서 진한 노드들은 종료 노드들로 해당 위치에 대응되는 문자열이 트라이가 집합에 표현되어 있다는 것을 의미합니다. BE, BET 등을 나타내는 노드들은 종료 노드지만 TE의 경우에는 그렇지 않습니다.
트라이에서 중요한 점은 루트에서 한 노드까지 내려가는 경로에서 만나는 글자들을 모으면 해당 노드에 대응되는 접두사를 얻을 수 있습니다. 즉 각 노드별로 대응되는 문자열을 저장할 필요가 없습니다.
트라이의 한 노드는 자손 노드들을 가리키는 포인터 목록과 이 노드가 종료 노드인지를 나타내는 불린 값 변수로 구성됩니다.
만약 모두 대문자로 이루어진 문자열을 저장하기 시작한다면 각 노드가 26개짜리 포인터 배열을 가지고 있으며, 0번은 A, 1번은 B와 같이 대응 될 것입니다. 하지만 이렇게 코드를 작성하면 메모리 낭비를 많이 하지만 다음 노드를 찾는 과정에서 어떤 탐색도 필요하지 않다는 장점이 있습니다.
const int ALPHABETS = 26;
int toNumber(char ch){ return ch - 'A'; }
struct TrieNode{
TrieNode* children[ALPHABETS];
bool terminal; //종료 노드인지 확인
TrieNode(): terminal(false){
memset(children, 0, sizeof(children));
}
~TrieNode(){
for(int i = 0; i < ALPHABETS; i++)
if(children[i])
delete children[i];
}
void insert(const char* key){
if(*key == 0)
terminal = true;
else{
int next = toNumber(*key);
if(children[next] == NULL) // 다음 노드가 NULL이라면 새로운 노드 생성
children[next] = new TrieNode();
children[next]->insert(key+1);
}
}
TrieNode* find(const char* key){
if(*key == 0) return this; //찾은 경우
int next = toNumber(*key);
if(children[next] == NULL) return NULL; // 못찾은 경우
return children[next]->find(key+1); // 다음글자 부터
}
}
find()함수는 찾는 문자를 모두 찾아서 마지막인 0이 나오면 this를 반환하고 못찾은 경우 다음 문자의 노드가 NULL일 때는 NULL을 반환해줍니다. 마지막 문자인지 확인하지 않으면 또 다른 효과가 있습니다. 문자열이 입력되는 중간에 자동 완성을 한다거나 하는 프로그램을 구현할 때 유용하게 사용됩니다.
시간 복잡도
find(), insert()의 시간 복잡도는 얼마일까요? 이 함수들은 문자열의 길이 만큼 재귀 호출을 수행하기 때문에 두 함수의 시간 복잡도는 모두 문자열의 길이 M에 선형 비례합니다. 이는 트라이에 얼마나 많은 문자열이 입력되었던 간에 크게 문제되지 않습니다.
한계점
트라이의 최대 문제는 필요로 하는 공간이 너무 큽니다. 알파벳 대문자만 저장한다고 해도 크라이의 각 노드는 26개의 포인터를 저장해야합니다. 즉 노드 하나를 표현하면 64비트 아키텍처에 포인터는 8바이트이니 26 * 8 200 바이트 가량을 사용해야합니다.
'Algorithm > 이론' 카테고리의 다른 글
| 올바른 이진 탐색 트리인지 확인하기 (0) | 2021.01.19 |
|---|---|
| KMP 알고리즘 (0) | 2020.07.17 |
| union-find(Disjoint-set) (0) | 2020.06.25 |
| 투포인터(two pointer) (4) | 2020.05.10 |
| 최단 경로(3) 벨만 포드 (0) | 2020.04.11 |